Несобственные интегралы. Признаки сходимости несобственных интегралов Несобственные интегралы с бесконечным верхним пределом

Как известно, нахождение интеграла может представлять собой достаточно сложную задачу. Было бы большим разочарованием заняться вычислением несобственного интеграла и обнаружить в конце пути, что он расходится. Поэтому представляют интерес методы, позволяющие без серьезных вычислений по одному виду функций сделать заключение о сходимости или расходимости несобственного интеграла. Первая и вторая теоремы сравнения, которые будут рассмотрены ниже, в значительной степени помогают исследовать несобственные интегралы на сходимость.

Пусть f(x)?0. Тогда функции

являются монотонно возрастающими от переменных t или-д (поскольку берем д>0, -д стремится к нулю слева). Если при возрастании аргументов функции F 1 (t) и F 2 (-д) остаются ограниченными сверху, это означает, что соответствующие несобственные интегралы сходятся. На этом основана первая теорема сравнения для интегралов от неотрицательных функций.

Пусть для функции f(x)и g(x) при x?a выполнены условия:

• 1) 0?f(x)?g(x);
• 2) Функции f(x) и g(x)непрерывны.

Тогда из сходимости интеграла следует сходимость интеграла, а из расходимости интеграла следует расходимость

Поскольку 0?f(x)?g(x) и функции непрерывны, то

По условию интеграл сходится, т.е. имеет конечную величину. Следовательно, интеграл сходится также.

Пусть теперь интеграл расходится. Предположим, что интеграл сходится, но тогда должен сходиться интеграл, что противоречит условию. Наше предположение неверно, интеграл расходится.

Теорема сравнения для несобственных интегралов 2-го рода.

Пусть для функций f(x) и g(x) на промежутке , неограниченно возрастает при x>+0. Для нее при x>+0 справедливо неравенство <. Несобственный интеграл есть эталонный интеграл 2-го рода, который при p=<1 сходится; следовательно, по 1-й теореме сравнения для несобственных интегралов 2-го рода интеграл сходится также.

Теорема сравнения для несобственных интегралов 1-го рода.

Пусть для функции f(x) и g(x) на промежутке $, оба этих числа ниже полагаются конечными. Если имеется всего 1 разрыв, он может находиться или в точке $a$, или в точке $b$, или внутри интервала $(a,\,b)$. Рассмотрим сначала случай, когда разрыв второго рода имеется в точке $a$, а в остальных точках подинтегральная функция непрерывна. Итак, мы обсуждаем интеграл

\begin{equation} I=\int _a^b f(x)\,dx, (22) \label{intr2} \end{equation}

причем $f(x) \rightarrow \infty $, когда $x \rightarrow a+0$. Как и ранее, прежде всего следует придать смысл этому выражению. Для этого рассмотрим интеграл

\[ I(\epsilon)=\int _{a+\epsilon}^b f(x)\,dx. \]

Определение. Пусть существует конечный предел

\[ A=\lim _{\epsilon \rightarrow +0}I(\epsilon)=\lim _{\epsilon \rightarrow +0}\int _{a+\epsilon}^b f(x)\,dx. \]

Тогда говорят, что несобственный интеграл второго рода (22) сходится, и ему приписывают значение $A$, саму функцию $f(x)$ называют интегрируемой на интервале $\left[ a, \, b\right]$.

Рассмотрим вариант, когда разрыв второго рода подинтегральной функции имеется на верхнем пределе интервала интегрирования. Этот случай можно свести к предыдущему, сделав замену переменной $x=-t$ и затем переставив пределы интегрирования.

Рассмотрим вариант, когда разрыв второго рода у подинтегральной функции имеется внутри интервала интегрирования, в точке $c \in (a,\,b)$. В данном случае исходный интеграл

\begin{equation} I=\int _a^bf(x)\,dx (23) \label{intr3} \end{equation}

представляют в виде суммы

\[ I=I_1+I_2, \quad I_1=\int _a^cf(x)\,dx +\int _c^df(x)\,dx. \]

Определение. Если оба интеграла $I_1, \, I_2$ сходятся, то несобственный интеграл (23) называют сходящимся и ему приписывают значение, равное сумме интегралов $I_1, \, I_2$, функцию $f(x)$ называют интегрируемой на интервале $\left[ a, \, b\right]$. Если хотя бы один из интегралов $I_1,\, I_2$ является расходящимся, несобственный интеграл (23) называют расходящимся.

Сходящиеся несобственные интегралы 2 рода обладают всеми стандартными свойствами обычных определенных интегралов.

1. Если $f(x)$, $g(x)$ интегрируемы на интервале $\left[ a, \,b \right ]$, то их сумма $f(x)+g(x)$ также интегрируема на этом интервале, причем \[ \int _a^{b}\left(f(x)+g(x)\right)dx=\int _a^{b}f(x)dx+\int _a^{b}g(x)dx. \] 2. Если $f(x)$ интегрируема на интервале $\left[ a, \, b \right ]$, то для любой константы $C$ функция $C\cdot f(x)$ также интегрируема на этом интервале, причем \[ \int _a^{b}C\cdot f(x)dx=C \cdot \int _a^{b}f(x)dx. \] 3. Если $f(x)$ интегрируема на интервале $\left[ a, \, b \right ]$, причем на этом интервале $f(x)>0$, то \[ \int _a^{b} f(x)dx\,>\,0. \] 4. Если $f(x)$ интегрируема на интервале $\left[ a, \, b \right ]$, то для любого $c\in (a, \,b)$ интегралы \[ \int _a^{c} f(x)dx, \quad \int _c^{b} f(x)dx \] тоже сходятся, причем \[ \int _a^{b}f(x)dx=\int _a^{c} f(x)dx+\int _c^{b} f(x)dx \] (аддитивность интеграла по интервалу).

Рассмотрим интеграл

\begin{equation} I=\int _0^{1}\frac{1}{x^k}\,dx. (24) \label{mod2} \end{equation}

Если $k>0$, подинтегральная функция стремится к $\infty$ при $x \rightarrow +0$, так что интеграл - несобственный второго рода. Введем функцию

\[ I(\epsilon)=\int _{\epsilon}^{1}\frac{1}{x^k}\,dx. \]

В данном случае первообразная известна, так что

\[ I(\epsilon)=\int _{\epsilon}^{1}\frac{1}{x^k}\,dx\,=\frac{x^{1-k}}{1-k}|_{\epsilon}^1= \frac{1}{1-k}-\frac{\epsilon ^{1-k}}{1-k}. \]

при $k \neq 1$,

\[ I(\epsilon)=\int _{\epsilon}^{1}\frac{1}{x}\,dx\,=lnx|_{\epsilon}^1= -ln \epsilon. \]

при $k = 1$. Рассматривая поведение при $\epsilon \rightarrow +0$, приходим к выводу, что интеграл (20) сходится при $k

10.2.2 Признаки сходимости несобственных интегралов 2 рода

Теорема (первый признак сравнения). Пусть $f(x)$, $g(x)$ - непрерывны при $x\in (a,\,b)$, причем $0 1. Если интеграл \[ \int _a^{b}g(x)dx \] сходится, то сходится и интеграл \[ \int _a^{b}f(x)dx. \] 2. Если интеграл \[ \int _a^{b}f(x)dx \] расходится, то расходится и интеграл \[ \int _a^{b}g(x)dx. \]

Теорема (второй признак сравнения). Пусть $f(x)$, $g(x)$ - непрерывны и положительны при $x\in (a,\,b)$, причем существует конечный предел

\[ \theta = \lim_{x \rightarrow a+0} \frac{f(x)}{g(x)}, \quad \theta \neq 0, \, +\infty. \]

Тогда интегралы

\[ \int _a^{b}f(x)dx, \quad \int _a^{b}g(x)dx \]

сходятся или расходятся одновременно.

Теорема 12.11 (признак сравнения несобственных интегралов). Пусть функции f(x) и g(x) непрерывны на промежутке [а, «>) и удовлетворяют на нем условию 0 fix) ?(х). Тогда из сходимости интеграла

следует сходимость интеграла

и наоборот, из расходимости интеграла (12.64) следует расходимость интеграла (12.63).

Доказательство. Введем обозначения:

Функция Р(К) является неубывающей; в самом деле, если а Я 2 , то

J fix) dx>0, и тогда

Возьмем последовательность значений {/?„} -> «>; тогда соответствующая последовательность значений функции {F(R n)} является монотонной и неубывающей. Пусть интеграл (12.63) сходится, тогда последовательность {67 (R it)} ограничена; но тогда ограничена и последовательность {F (/?„)}, а значит, в силу теоремы 7.13 она сходится. Следовательно, существует предел F (R) при R -+ «>, т.е. интеграл (12.64) сходится.

Теперь докажем вторую часть теоремы; пусть интеграл (12.64) расходится. Если предположить, что интеграл (12.63) сходится, то по доказанному выше интеграл (12.64) также должен сходиться, что противоречит условию. Теорема доказана. ?

Замечание. Аналогичный признак сравнения справедлив и для несобственных интегралов второго рода. Если функции /(х) и g (х) непрерывны на полуинтервале [а> b) и для всех точек в некоторой окрестности особой точки b выполнены

условия 0 (х), то из сходимости интеграла Jg(x)dx следует сходи-

мость интеграла J/(x)dx, а из расходимости интеграла J/(x)dx - расходи-

мость интеграла Jg(x)dx.

Рассмотрим примеры на исследование сходимости несобственных интегралов.

Пример 27. Т . ^-.

Х 3 (1 + е Л)

Решение. Сравним подынтегральную функцию в этом интеграле с функцией

Дг. Очевидно, что -г- -

х г* (1+0 x J

грал J-jdx сходится; следовательно, в силу признака сравнения сходится и дан- 1 х

ный интеграл.

Пример 28. I-.

Решение. Сравнивая подынтегральную функцию этого интеграла с функцией 1/х,

видим, что (1 + In х)/х > 1/х на промежутке 1

дится, следовательно, по признаку сравнения расходится и данный интеграл.

В заключение приведем без доказательства критерий Коши сходимости несобственного интеграла первого рода.

12.10.4. Абсолютная и условная сходимость несобственных интегралов

Определение 5. Несобственный йнтеграл J/(x)dx называется абсолютно

сходящимся , если сходится интеграл J|/(x)|dx.

Определение 6. Несобственный интеграл J /(х) dx называется условно схо-

дящимся , если он сходится, а интеграл J|/(x)|dx расходится.

Заметим, что из абсолютной сходимости интеграла следует и его сходимость в силу оценки 3 определенного интеграла и критерия Коши.

Теорема 12.13 (признак Дирихле - Абеля*). Пусть функция/(х) непрерывна и имеет ограниченную первообразную F (х) на промежутке [а, «>), а функция g(x) имеет непрерывную производную на этом промежутке, не возрастает и стремится к нулю при х -> ©о. Тогда несобственный интеграл

сходится.

Доказательство. Применим интегрирование по частям к интегралу J /(x)g(x)dx

на произвольном отрезке R R" с [а , °°). Имеем:

Теорема 12.12. Для сходимости несобственного интеграла (12.64) необходимо и достаточно, чтобы для любого е > 0 можно найти такое число А > 0, что для любых R" и /?", больших, чем А, выполняется неравенство:

По условию теоремы F(x) ограничена, т.е. |F(x)| К. Функция g(x) не возрастает и стремится к нулю при х -» «>, значит. g(x) > 0, a g"(x)

Абель Нильс Хенрик (1802-1829) - норвежский математик.

Поскольку по условию теоремы g(x) -» 0 при х -> ©°, для произвольного числа е > 0 можно найти число А> такое, что при R" > Л будет выполнено неравенство g(R") Подставляя это в оценку (12.68), получаем:

что соответствует критерию Коши сходимости интеграла (12.66). Теорема доказана. ?

Рассмотрим примеры использования признака Дирихле - Абеля сходимости несобственных интегралов.

Пример 29. f^^dx, а>0.

Решение. Положим /(х) = sin х, g(x) = l/x"; легко убедиться, что все условия теоремы выполнены, т.е. данный интеграл сходится. При а > 1 данный интег-

рал сходится абсолютно. Действительно, |sin х/хР 1/д Л, интеграл J(l/x e)dx

сходится, т.е. по признаку сравнения (теорема 12.11) сходится абсолютно и данный интеграл.

Пример 30. Jsin х 2 dx - интеграл Френеля, о

Решение. Представим этот интеграл в виде суммы:

Поскольку sin х 2 - непрерывная функция на отрезке (0, 1J, первый интеграл в (12.69) существует. Для выяснения сходимости несобственного интеграла в правой части (12.69) положим/(х) = х sin х 2 , g (х) = 1/х. Тогда для функции /(х) первообразная F(x) = -cosx 2 /! ограничена на промежутке |1, «>), а#(х) - положительна, стремится к нулю при х -» °° и имеет непрерывную производную на (1, ©о). Значит по признаку Дирихле - Абеля второй интеграл в (12.69) сходится, т.е. интеграл Френеля также сходится.

Несобственные интегралы первого рода. По сути это тот же определённый интеграл, но в случаях, когда интегралы имеют бесконечный верхний или нижний пределы интегрирования, или оба предела интегрирования бесконечны.

Несобственные интегралы второго рода. По сути это тот же определённый интеграл, но в случаях, когда интеграл берётся от неограниченных функций, подынтегральная функция в конечном числе точек конечного отрезка интегрирования не имеет, обращаясь в бесконечность.

Для сравнения. При введении понятия определённого интеграла предполагалось, что функция f (x ) непрерывна на отрезке [a , b ], а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью. Некоторые задачи приводят к необходимости отказаться от этих ограничений. Так появляются несобственные интегралы.

Геометрический смысл несобственного интеграла выясняется довольно просто. В случае, когда график функции y = f (x ) находится выше оси Ox , определённый интеграл выражает площадь криволинейной трапеции, ограниченной кривой y = f (x ) , осью абсцисс и ординатами x = a , x = b . В свою очередь несобственный интеграл выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями y = f (x ) (на рисунке ниже - красного цвета), x = a и осью абсцисс.

Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:

Площадь бесконечной криволинейной трапеции может быть конечным числом и в этом случае несобственный интеграл называется сходящимся. Площадь может быть и бесконечностью и в этом случае несобственный интеграл называется расходящимся.

Использование предела интеграла вместо самого несобственного интеграла. Для того, чтобы вычислить несобственный интеграл, нужно использовать предел определённого интеграла. Если этот предел существует и конечен (не равен бесконечности), то несобственный интеграл называется сходящимся, а в противном случае - расходящимся. К чему стремится переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода или второго рода. Узнаем об этом сейчас же.

Несобственные интегралы первого рода - с бесконечными пределами и их сходимость

Несобственные интегралы с бесконечным верхним пределом

Итак, запись несобственного интеграла как отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен.

Определение. Несобственным интегралом с бесконечным верхним пределом интегрирования от непрерывной функции f (x ) на промежутке от a до ∞ называется предел интеграла этой функции с верхним пределом интегрирования b и нижним пределом интегрирования a при условии, что верхний предел интегрирования неограниченно растёт , т.е.

.

Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся , а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся и ему не приписывается никакого значения.

Пример 1. Вычислить несобственный интеграл (если он сходится).

Решение. На основании определения несобственного интеграла находим

Так как предел существует и равен 1, то и данный несобственный интеграл сходится и равен 1.

В следующем примере подынтегральная функция почти как в примере 1, только степень икса - не двойка, а буква альфа, а задача состоит в исследовании несобственного интеграла на сходимость. То есть предстоит ответить на вопрос: при каких значениях альфы данный несобственный интеграл сходится, а при каких расходится?

Пример 2. Исследовать на сходимость несобственный интеграл (нижний предел интегрирования больше нуля).

Решение. Предположим сначала, что , тогда

В полученном выражении перейдём к пределу при :

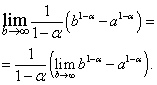
Нетрудно видеть, что предел в правой части существует и равен нулю, когда , то есть , и не существует, когда , то есть .

В первом случае, то есть при имеет место . Если , то и не существует.

Вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходится при .

Применяя к изучаемому виду несобственного интеграла формулу Ньютона-Лейбница , можно вывести следующую очень похожую на неё формулу:

.

Это обобщённая формула Ньютона-Лейбница.

Пример 3. Вычислить несобственный интеграл (если он сходится).

Предел этого интеграла существует:

Второй интеграл, составляющий сумму, выражающую исходный интеграл:

Предел этого интеграла также существует:

.

Находим сумму двух интегралов, являющуюся и значением исходного несобственного интеграла с двумя бесконечными пределами:

Несобственные интегралы второго рода - от неограниченных функций и их сходимость

Пусть функция f (x ) задана на отрезке от a до b и неограниченна на нём. Предположим, что функция обращается в бесконечность в точке b , в то время как во всех остальных точках отрезка она непрерывна.

Определение. Несобственным интегралом функции f (x ) на отрезке от a до b называется предел интеграла этой функции с верхним пределом интегрирования c , если при стремлении c к b функция неограниченно возрастает, а в точке x = b функция не определена , т.е.

.

Если этот предел существует, то несобственный интеграл второго рода называется сходящимся, в противном случае - расходящимся.

Используя формулу Ньютона-Лейбница, выводим.